Question

A substance decays according to A = Ae-0.057, where I is in hours and Ao is the initial amount. Determine the half-life of the substance. Round your answer to two

decimal places, if necessary.

Answer 1

12.16 hours

Explanation:

I'm going to assume my assumption is right.

You can let me know differently.

`A=A_0 \cdot e^(-0.057t)`

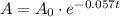
We want to know the time, t, such that A will be half it's initial population.

This means we want to solve the following equation for t:

`(A_0)/(2)=A_0 \cdot e^(-0.057t)`

Divide both sides by
`A_0`:

`(1)/(2)=e^(-0.057t)`

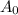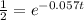
Now we are ready to try to get the variable by itself.

Let's rewrite in the equivalent logarithm form:

`\ln((1)/(2))=-0.057t`

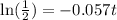
Divide both sides by -0.057:

`(\ln((1)/(2)))/(-0.057)=t`

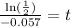
Put left hand side into a calculator:

`12.16=t`

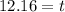
So the half-life is 12.16.

This means that the initial population will be brought down to half of the initial population in 12.16 hours approximately.