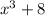Answer:
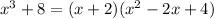
So if they meant
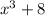 then the answer is:
then the answer is:
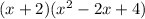 .
.
The choice this corresponds to is A.
Explanation:
The sum of cubes formula for factoring or expanding:
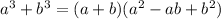
You have I'm assuming they meant:
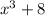 .
.
Compare
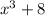 to
to
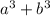 .
.
You should see in place of
 you have
you have
 .
.
You should also see in place of
 you have
you have
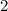 .
.
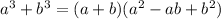
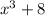
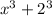
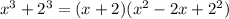
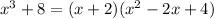
Let's check it for fun.
So we are going to use the distributive property.
We are going to distribute all the terms in the first ( ) to all the terms in the second ( ).
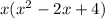 +
+
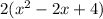
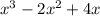 +
+
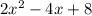
Combine like terms:
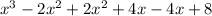
Simplify the grouping of like terms:
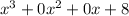
0 times anything is 0: