Answer:
The term a15 of the sequence is
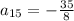 .
.
Explanation:
The given sequence is
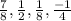
It it an arithmetic sequence because the difference between two consecutive terms are same.
The first term of the given AP is
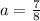
The common difference is
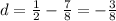
The nth term of an AP is
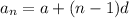
where, a is first term and d is common difference.

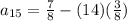
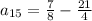
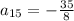
Therefore the term a15 of the sequence is
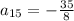 .
.