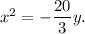Answer: The required equation of the parabola is
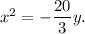
Step-by-step explanation: We are given to write the equation for a parabola with focus
 and directrix
and directrix
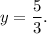
Since the focus of the parabola lies on the y-axis, so the equation of the parabola is of the following form :

And, the directrix is
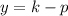 and the focus is (h, k+p).
and the focus is (h, k+p).
According to the given information, we have

Adding equations (ii) and (iii), we get
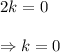
and
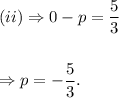
Substituting the values of h, k and p in equation (i), we get
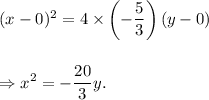
Thus, the required equation of the parabola is