Answer:
The volume of the cone in terms of π is:
A. 392π in³
Explanation:
The radius of the cone i.e. r is: 7 in.
and the slant height of the cone i.e. l=y=25 in.
and let h=x be the height of the cone.
Now, using the Pythagorean Theorem we have:
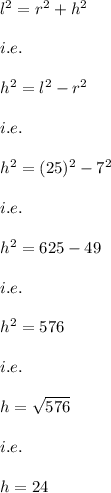
Hence, we get:
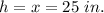
Now, the volume of the cone is given by:
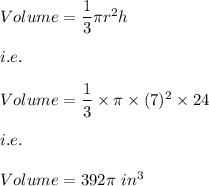
Hence, the answer is: Option: A