Question

Write an expression that can be usedto find the nth termo of each sequence 9, 17, 25, 33

Answer 1

The expression used to find the nth term of each sequence 9, 17, 25, 33 will be:

• 
  `a_n=8n+1`

Explanation:

Given the sequence

9, 17, 25, 33

a₁ = 9

Determining the common difference

d = 17-9 = 8

d = 25-17 = 8

d = 33-25 = 8

As the common difference between the adjacent terms is same and equal to

d = 8

Therefore, the given sequence is an Arithmetic sequence.

An arithmetic sequence has a constant difference 'd' and is defined by

`a_n=a_1+\left(n-1\right)d`

substituting a₁ = 9, d = 8 in the equation

`\:a_n=9+8n-8`

`a_n=8n+1`

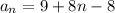
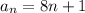
Therefore, the expression used to find the nth term of each sequence 9, 17, 25, 33 will be:

• 
  `a_n=8n+1`