Question

What is the discontinuity and zero of the function f(x)= 3x^2+x-4/x-1

A) discontinuity at (-1,1), zero at (4/3,0)
B) discontinuity at (-1,1), zero at (-4/3,0)
C)discontinuity at (1,7), zero at (4/3,0)
D)discontinuity at (1,7), zero at (-4/3, 0)

Answer 1

D.

Explanation:

To find the discontinuity given this is a fraction, we only have to worry about dividing by 0.

So we only have to worry about x-1 being 0.

x-1=0

Add 1 on both sides gives:

x=1

So there is a discontinuity when x=1.

Now there cannot also be a zero at this number since the function doesn't exist there.

However if you plug 1 into the fraction before simplification any you get 0/0 then you have a hole at x=1.

`(3(1)^2+(1)-4)/(1-1)=(3+1-4)/(0)=(4-4)/(0)=(0)/(0)`.

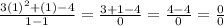So we do indeed have a hole at x=1.

To find point that would make this function continuous at x=1, we will simplify our fraction and then plug in 1:

I already know x-1 is a factor of the top because x=1 made it zero on top:

`((x-1)(3x+4))/(x-1)`

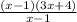
The (x-1)'s cancel:

`(3x+4)`

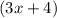
Now 3x+4 evaluated at x=1 gives 3(1)+4=3+4=7.

So the hole is at (1,7).

The choice is either C or D.

The zero is when 3x+4 is 0.

This is the numerator after simplification. The top of the fraction is what determines if the fraction itself will be 0 since 0/anything is 0 except when you are dividing by 0.

3x+4=0

Subtract 4 on both sides gives:

3x=-4

Divide both sides by 3:

x=-4/3

So the zero is at (-4/3,0).