Question

I really need help understanding this question! thank you!

The product of two consecutive positive integers is 42. Write and solve a quadratic equation to find the solutions. Then show how you use those solutions to find the two consecutive positive integers.

Answer 1

`n(n+1)=42\\n^2+n-42=0\\n^2-6n+7n-42=0\\n(n-6)+7(n-6)=0\\(n+7)(n-6)=0\\n=-7 \vee n=6`

-7 is not positive

`n=6\\n+1=7`

The numbers are 6 an 7.

Answer 2

`\boxed{\text{6 and 7}}`

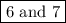
Explanation:

1. Set up the equation

Let x = the first integer. Then

x + 1 = the next integer

x(x + 1) = the product of the integers

x(x + 1) = 42

x² + x = 42 Distributed the x

x² + x - 42 = 0

2. Solve for x

(x + 7)(x - 6) = 0 Factored the quadratic

x + 7 = 0 x - 6 = 0 Applied zero product rule

x = -7 x = 6 Solved the binomials

We reject x = -7, because x must be positive

x = 6

x + 1 = 7

`\text{The two consecutive positive integers are \boxed{\textbf{6 and 7}}}`

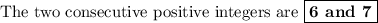
Check:

6(6+ 1) = 42

6(7) = 42

42 = 42

OK.