Question

A ball is thrown upward from a height of 15ft with an initial upward velocity of 5ft/s. Use the formula h=-16t2(t Is squared)+ vt + s to find how long it will take for the ball to hit the ground .

Answer 1

The ball has hit the ground in about 1.137 seconds.

Explanation:

The ball has hit the ground when the height between the ball and the ground is 0. So we will be setting h equal to 0 and then solving this equation for t.

h=-16t^2+vt+s

v represents the initial velocity

s represents the initial height

v is given as 5ft/s.

s is given as 15ft.

Inputting these in result in:

h=-16t^2+5t+15

Now we are finding for what t's do we have h=0:

0=-16t^2+5t+15

Let's calculate the discriminant to predict how messy are answers are going to be.

Discriminant=b^2-4ac

Discriminant=(5)^2-4(-16)(15)

Discriminant=25+960

Discriminant=985

It isn't a perfect square so we can't factor this.

I'm going to use the quadratic formula:

`t=\frac{-b \pm \sqrt{\text{Discriminant}}}{2a}`

`t=(-5 \pm √(985))/(2(-16))`

`t=(-5 \pm √(985))/(-32)`

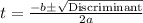
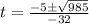
This implies we have two values for t to look at when h=0:

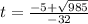`t=(-5+√(985))/(-32)` or
`t=(-5-√(985))/(-32)`

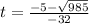
Inputting both of these into the calculator:

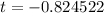`t=-0.824522` or
`t=1.137022`

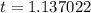
So the answer that makes sense here is the later answer.

The ball has hit the ground in about 1.137 seconds.

Answer 2

1.137 Seconds

Explanation:

Substitute new number into the formula like so:

-16t^2+5t+15

Then using the new formula just plug into the quadratic equation and you should get two answer like:

-0.825, 1.137

Since you can't really have negative a distance you would drop -0.825 cuz it wouldn't really make sense.

So the solution would be 1.137 seconds :)

Hope I helped xaditinairx on insta