Question

The sum of two integers is 56 and their difference is 4. what are the two integers

Answer 1

`x+y=56,\:x-y=4\quad :\quad y=26,\:x=30`

Explanation:

`\star\star\star\star~\textrm{Let the two integers be x and y respectively.}~\star\star\star\star`

`\textrm{Then, our equations will look like;}`

`\begin{bmatrix}x+y=56\\ x-y=4\end{bmatrix}`

`\black{\mathrm{Isolate}\:x\:\mathrm{for}\:x+y=56:}`

`x+y=56`

`\gray{\mathrm{Subtract\:}y\mathrm{\:from\:both\:sides}}`

`x+y-y=56-y`

`\gray{\mathrm{Simplify}}`

`x=56-y`

`\gray{\mathrm{Subsititute\:}x=56-y}`

`\begin{bmatrix}56-y-y=4\end{bmatrix}`

`\black{\mathrm{Isolate}\:y\:\mathrm{for}\:56-y-y=4:}`

`56-y-y=4`

`\gray{\mathrm{Add\:similar\:elements:}\:-y-y=-2y}`

`56-2y=4`

`\gray{\mathrm{Subtract\:}56\mathrm{\:from\:both\:sides}}`

`56-2y-56=4-56`

`\gray{\mathrm{Simplify}}`

`-2y=-52`

`\gray{\mathrm{Divide\:both\:sides\:by\:}-2}`

`\displaystyle(-2y)/(-2)=(-52)/(-2)`

`\gray{\mathrm{Simplify}}`

`y=26`

`\gray{\mathrm{For\:}x=56-y}`

`\gray{\mathrm{Subsititute\:}y=26}`

`x=56-26`

`\gray{56-26=30}`

`x=30`

`\gray{\mathrm{The\:solutions\:to\:the\:system\:of\:equations\:are:}}`

`y=26,\:x=30`

`\blue{\mathrm{Plotting:}~x+y=56,\:x-y=4}`

Answer 2

Let
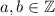`a,b\in\mathbb{Z}` then we have a system of equations.

First the sum of a and b is 56.

a + b = 56

Second the difference of a and b is 4.

a - b = 4

From here our system of equations is,

`a+b=56\wedge a-b=4`

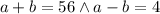
We can solve it using the elimination. If you add both of the equations the b terms cancel out hence,

`2a=60\Longrightarrow a=30`

Now that we have a value of a we can calculate b. Just pick one equation from the system.

`30-b=4\Longrightarrow b=26`

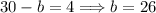
And the solutions to the system are two positive integers
`\underline{a=30},\underline{b=26}`

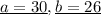
Hope this helps!