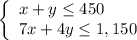Answer:
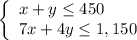
Explanation:
Let x be the number of adults and y be the number of campers.
There are rooms for 450 people, so
x+y≤450.
Each adult costs $7, then x adults cost $7x.
Each camper costs $4, then y campers cost $4y.
There is a maximum budget of $1,150, so
7x+4y≤1,150
Hence, you get the system of two inequalities: