Question

Solve the system of equations using substitution or elimination by addition.

x + y = 0.5
0.7x + 0.6y = 0.31

Select the correct choice below and if necessary, fill in the answer box to complete your choice.

A.The solution is ___ ​(Type an ordered​ pair.)
B.There are infinitely many solutions.
C.There is no solution.

Answer 1

a. (0.1,0.4)

Explanation:

Answer 2

Answer: A. The unique solution to the system is
`(0.1,0.4)`

Explanation:

You can follow these steps to solve the system of equation by the Elimination Method:

- Multiply the first equation by -0.7, then add both equations and solve for "y":

`\left \{ {-0.7(x + y) =-0.7(0.5)} \atop {0.7x + 0.6y = 0.31}} \right.\\\\\left \{ {-0.7x-0.7y =-0.35} \atop {0.7x + 0.6y = 0.31}} \right.\\............................\\-0.1y=-0.04\\\\y=0.4`

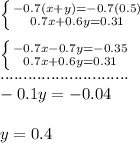
- Substitute the value of "y" into any original equation to find the value of "x". Then:

`x + (0.4) = 0.5\\\\x=0.5-0.4\\\\x=0.1`

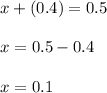
Therefore, the unique solution to the system is
`(0.1,0.4)`