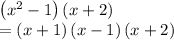Question

Some steps to rewrite the expression x3 − x + 2x2 − 2 as a product of three factors are shown below:

Step 1: x3 − x + 2x2 − 2
Step 2: x3 + 2x2 − x − 2
Step 3: x2(x + 2) − 1(x + 2)

Which of the following best shows the next two steps to rewrite the expression?

Step 4: (x2 + 1)(x + 2); Step 5: (x + 1)(x + 1)(x + 2)
Step 4: (x2 − 1)(x + 2); Step 5: (x − 1)(x + 1)(x + 2)
Step 4: (x2 − 1)(x + 2); Step 5: (x + 1)(x + 1)(x + 2)
Step 4: (x2 + 1)(x + 2); Step 5: (x − 1)(x + 1)(x + 1)

Answer 1

The second one

Explanation:

From step 3, that is

x²(x + 2) - 1 (x + 2) ← factor out (x + 2) from each term

= (x + 2)(x² - 1) ← step 4

x² - 1 is a difference of squares and factors as

x² - 1) = (x - 1)(x + 1)

Hence from step 4 we obtain

(x + 2)(x - 1)(x + 1) ← step 5

Answer 2

`\left ( x^2-1 \right )\left ( x+2 \right )\\=\left ( x+1 \right )\left ( x-1 \right )\left ( x+2 \right )`

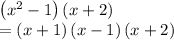
Explanation:

Algebraic expression is an expression consists of variables and constants which are combined using algebraic operations: + , - , × , ÷ .

Here, we are required to simplify algebraic expression:
`x^3-x+2x^2-2`

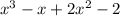
Three steps are given as :

`x^3-x+2x^2-2\\=x^3+2x^2-x-2\\=x^2\left ( x+2 \right )-1\left ( x+2 \right )`

We need to find the next two steps:

Next step is
`\left ( x^2-1 \right )\left ( x+2 \right )`

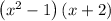
We will use formula:
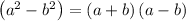`\left ( a^2-b^2 \right )=\left ( a+b \right )\left ( a-b \right )` to write
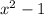`x^2-1` as
`\left ( x+1 \right )\left ( x-1 \right )`

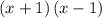
Therefore, we get next two steps as follows:

`\left ( x^2-1 \right )\left ( x+2 \right )\\=\left ( x+1 \right )\left ( x-1 \right )\left ( x+2 \right )`