Question

1.)

a^2b^3
---------- <-----write in expanded form.
cd


2.)what is the exact solution to the equation 4^5x=3^x-2

Please show all work I've been struggling to understand these questions!!!! thank you so much <3

Answer 1

1. Expanded form of
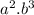`a^(2) . b^(3)` = (a.a).(b.b.b)

2.Exact solution x = -0.376

Explanation:

Solution:

First we have to write the Expanded Form of
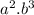`a^(2) . b^(3)`, Let's do it.

1)
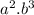`a^(2) . b^(3)` = (a.a).(b.b.b)

Hence,

Expanded form of
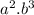`a^(2) . b^(3)` = (a.a).(b.b.b)

2)
`4^(5x) = 3^(x-2)`

Now, we have to find out the exact solution of the above equation:

In order to equate the exponents, we need to make sure the bases are same. Or we simply can use logarithm to solve the above equation.

So,

We are using logarithm to solve this equation.

Let's break this down:

`4^(5x) = 3^(x-2)`

Taking log on both sides.

log
`4^(5x)` = log
`3^(x-2)`

`5xlog(4)` =
`(x-2)log(3)`

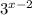
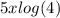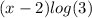
Dividing both sides by log(4)

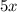`5x` = (x-2)
`(log(3))/(log(4))`

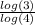
value of log(3) = 0.4771

value of log(4) = 0.6020

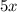`5x` = (x-2)
`(log(0.4771))/(log(0.6020))` =

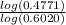5x = (x-2)0.792

5x = 0.792x - 1.584

by rearranging the equation, we get:

0.792x - 5x = 1.584

x(0.792 - 5) = 1.584

x(-4.208) = 1.584

x = -1.584/4.208

x = -0.376

Exact solution x = -0.376