Question

For 7 and 8 what could the pattern of each row/column be

Answer 1

Explanation:

For #7 use the coordinate points (3, 12) and (-2, 4) to find the slope between those 2 points. Then use the coordinate points (-2, 4) and (-12, -12) and find the slope between those 2 points just to make sure this is in fact a line. Assuming it is, the slopes will be the same.

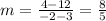`m=(4-12)/(-2-3)=(8)/(5)` and for the next pair:

`m=(-12-4)/(-12-(-2))=(-16)/(-10)=(8)/(5)`

The slope of the line in #7 is 8/5 or 1.6

For #8, we will use 2 pairs of coordinates just like above, then we will choose one of those coordinates, write the equation for the line, then make some subsitutions to solve for x and y values. First the slope:

Use coordinate pairs (2, 4) and (-1, 8):

`m=(8-4)/(-1-2)=-(4)/(3)`

We will use another 2 coordinate pairs and do the same thing just to make sure this is linear:

Use coordinate pairs (-10, 20) and (-19, 32):

`m=(32-20)/(-19-(-10))=-(12)/(9)=-(4)/(3)`

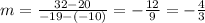
Ok so this is a line since the slopes are the same between the points. Now we will use one of those coordinates along with the slope to find the equation for this particular line. Let's use (2, 4) and m = -4/3:

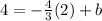`4=-(4)/(3)(2)+b` and

`4=-(8)/(3)+b`

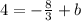
Let's multiply everything by 3 to get rid of the fraction:

12 = -8 + 3b and

20 = 3b so

`b=(20)/(3)`

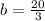
Our equation then is

`y=-(4)/(3)x+(20)/(3)`

We will sub in an x value of 5 to find the corresponding y value:

`y=-(4)/(3)(5)+(20)/(3)` and

`y=-(20)/(3)+(20)/(3)` so

y = 0

For the next x value of -7:

`y = -(4)/(3)(-7)+(20)/(3)` so

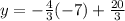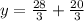`y=(28)/(3)+(20)/(3)` so

y = 16

Now to sub in a y value to find x:

`24=-(4)/(3)x+(20)/(3)`

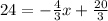
Multiply everything by 3 to get rid of the fractions:

72 = -4x + 20 and

52 = -4x so

x = -13

The missing coordinates are (5, 0); (-7, 16); and (-13, 24)