Answer:
Part A)
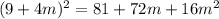
Part B)
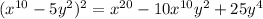
Part C)
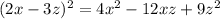
Part D)
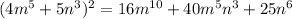
Part E)
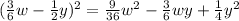
Part F)
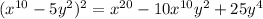
Explanation:
The question in English is
Calculate the square of each binomial
we know that
The square of a binomial is always a trinomial
so
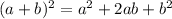
and
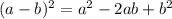
Part A) we have
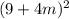
Applying the formula
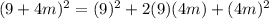
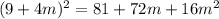
Part B) we have
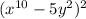
Applying the formula
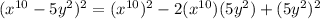
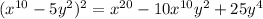
Part C) we have
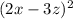
Applying the formula
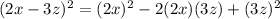
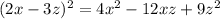
Part D) we have
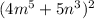
Applying the formula
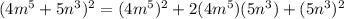
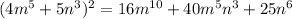
Part E) we have

Applying the formula
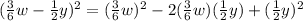
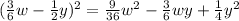
Part F) we have
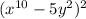
Applying the formula
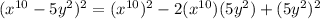
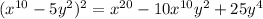
Note the problem F is the same problem B