Question

What is the recursive formula for the sequence?
15, 26, 48, 92, ...

Answer 1

`f(n)-f(n-1)=11(2)^(n-2)`

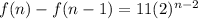
where f(1)=15.

Explanation:

I tried finding the 1st difference of the terms:

26-15,48-26,92-48

11,22,44

I noticed a pattern here in the 1st difference. To get the next term in this sequence you have to double the previous.

So the first difference sequence is geometric with first term 11 and common ratio 2. The explicit form for a geometric sequence is
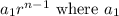`a_1 r^(n-1) \text{ where } a_1` is the first term and r is common ratio.

So we have this:

`\text{Term}-\text{Previous}=11(2)^(n-1)`

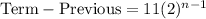
More formally:

`f(n)-f(n-1)=11(2)^(n-1)`

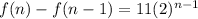
where f(1)=15.

Lets test it.

We want to finf f(2) in hopes of being 26:

We replace n with 2:

`f(2)-f(2-1)=11(2)^(2-1)`

`f(2)-f(1)=11(2)^(1)`

`f(2)-15=11(2)`

`f(2)-15=22`

`f(2)=37`

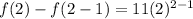
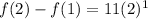
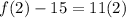
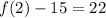
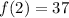
This is a little high for the second term. We are going to tweak our exponent on the geometric sequence part because it is one term ahead of where we are in our sequence.

`f(n)-f(n-1)=11(2)^(n-2)`

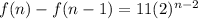
where f(1)=15.

Let's try this again:

`f(2)-f(2-1)=11(2)^(2-2)`

`f(2)-f(1)=11(2)^(0)`

`f(2)-15=11(1)`

`f(2)-15=11`

`f(2)=26`

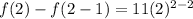
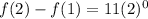
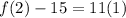
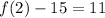
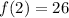
That is our 2nd term.

Let's do it again for our third term when n=3:

`f(3)-f(3-1)=11(2)^(3-2)`

`f(3)-f(2)=11(2)^(1)`

`f(3)-26=11(2)`

`f(3)-26=22`

`f(3)=48`

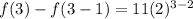
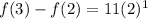
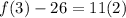
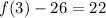
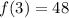
This is our third term.

One more check for n=4.

`f(4)-f(4-1)=11(2)^(4-2)`

`f(4)-f(3)=11(2)^(2)`

`f(4)-48=11(4)`

`f(4)-48=44`

`f(4)=92`

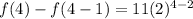
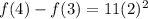
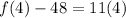
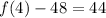
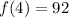
This is our fourth term.

Our recursive form for the given sequence works since we were able to generate each one using it.