Question

How do you solve this problem?

Answer 1

The arcs
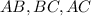`AB, BC, AC` all equal to the third of the perimeter since equilateral triangle divides them like this.

So we need to find a perimeter but we are only given the area.

Let's review,

`</p><p>A=\pi r^2 \\</p><p>P=2\pi r</p><p>`

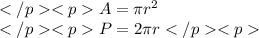
That means that from area we area able to calculate radius.

`A=\pi r^2\Longrightarrow r=\sqrt{(A)/(\pi)}`

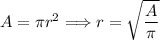
Insert the numbers,

`r=\sqrt{(36\pi)/(\pi)}=6`

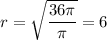
Then use the perimeter formula to calculate perimeter since radius is known,

`P=2\pi\cdot6=12\pi`

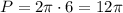
Now divide perimeter by 3 to get length of AB arc.

`AB=(12\pi)/(3)=\boxed{4\pi}`

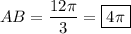
Hope this helps.