Question

A circle is inscribed in a square. A point in the figure is selected at random. Find the probability that the point will be in the part that is NOT shaded.

A.25%
B.10%
C.20%
D.5%

Answer 1

i think so 5%

\\

Explanation:

Answer 2

Answer: The correct option is (C) 20%.

Step-by-step explanation: Given that a circle is inscribed in a square and a point in the figure is selected at random.

We are to find the probability that the point will lie in the part that is NOT shaded.

Let a units be the side length of the square.

Then, the area of the square will be

`A_s=a^2.`

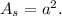
Also, the radius of the circle is equal to the half of the side length of the square. So, the area of the circle will be

`A_c=\pi \left((a)/(2)\right)^2=(22)/(7)*(a^2)/(4)=(11)/(14)a^2.`

So, the area of the part that is not shaded is given by

`A_(ns)=A_s-A_c=a^2-(11)/(14)a^2=(3)/(14)a^2.`

Therefore, the probability that the selected point is not in the shaded part is given by

`p=(A_(ns))/(A_s)*100\%=((3)/(14)a^2)/(a^2)*100\%=(300)/(14)\%=21.42\%(approx.)`

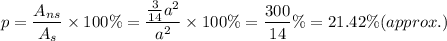
Thus, the required probability is 20%.

Option (C) is CORRECT.