Question

Someone please help me with this I really don’t know how to do this.

Answer 1

Slope of the graph is steeper.

The answer is:
`\mathbf{Slope=(1)/(3)}`

Explanation:

First we will find slope of the graph.

The formula used to find slope is:
`Slope=(y_2-y_1)/(x_2-x_1)`

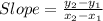
We need to find two points from the graph to find the slope.

Let we take point 1 (-2,1) and point 2 (1,2)

We will have:
`x_1=-2, y_1=1, x_2=1, y_2=2`

Now finding slope of the graph

`Slope=(y_2-y_1)/(x_2-x_1)\\Slope=(2-1)/(1-(-2)) \\Slope=(2-1)/(1+2)\\Slope=(1)/(3)`

So, slope of the graph is:
`\mathbf{Slope=(1)/(3)}`

Now, we will find slope of Linear function.

It has x-intercept of 1 and y-intercept of -2

x-intercept means y=0

So, the point will be: (1,0)

y-intercept means x=0

So, the point will be: (0,-2)

We will have:
`x_1=1, y_1=0, x_2=0, y_2=-2`

Putting values and finding slope

`Slope=(y_2-y_1)/(x_2-x_1)\\Slope=(-2-0)/(0-(1)) \\Slope=(-2-0)/(0+1)\\Slope=(-2)/(1)\\Slope=-2`

So, the slope of linear function is:
`\mathbf{Slope=-2}`

Now, we need to find which of the slope is steeper.

The larger the value of slope, more steeper it is:

Now, comparing the slopes:

The slope of the graph is:
`\mathbf{Slope=(1)/(3)}`

The slope of linear function is:
`\mathbf{Slope=-2}`

We know that,
`(1)/(3)>-2`

So, Slope of the graph is steeper.

The answer is:
`\mathbf{Slope=(1)/(3)}`