Question

Please explain your answer. Thank you.

Answer 1

See step-by-step

Explanation:

PQ = PS . Given

QR = SR . Given

PR = PR . Reflexive Property of Congruence

PQR = PSR SSS Congruence Theorem

Answer 2

(a) Used SSS congruence theorem.

(b) Orthocenter is (5,1)

Explanation:

(a) We have given PQ = PS and QR = SR.

Also, due to commonly, the third side of each triangle is the same (PR)

We have the same side length for three sides of both triangles. Let's apply SSS congruence rule.

Thus, both triangles are congruent.

(b) Given data:

Y = (3,-2)

A = (3,5)

B = (9,1)

We need to construct at least two slopes of the line equations. Let's have
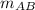`m_(AB)` and
`m_(YB)`

`m_(AB) = (5-1)/(3-9) = (4)/(-6) = -(2)/(3) \\m_(BY) = (-2-1)/(3-9) = (-3)/(-6) = (1)/(2)`

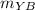
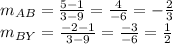
Now, let's have the slopes for their respective orthogonal lines:
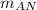`m_(AN)` and
`m_(YM)`

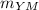
Let's remember that the product of orthogonal slopes is -1. Thus, for example
`m_(AN) m_(YB)=1 \\m_(YM) m_(AB)=1`

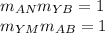
We will use the coordinates of A and AN slope:

For AN
`m_(AN) = -(1)/(YB) = -2\\-2 = (y-5)/(x-3)\\ y = -2x + 11`

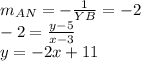
This was the equation of AN.

Now, for YM, will use the coordinates of Y and YM slope:

`m_(YM) = -(1)/(AB) = 3/2\\-3/2 = (y+2)/(x-3)\\ 2y-3x=13`

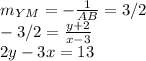
This was for YM.

The orthocenter will be found by resolving the two-variable linear equation:
`y = -2x+11\\2y-3x=-13\\2(-2x+11) -3x=-13\\-4x+22-3x=-13\\-7x=-13-22=-35\\x=5\\y=-10+11=1\\`

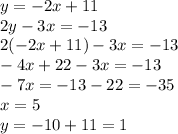
Thus, the orthocenter coordinates are (5,1)