Answer:
(16, 0) and (0,
 )
)
Explanation:
Given
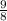 x + 8y = 18
x + 8y = 18
Multiply through by 8 to eliminate the fraction
9x + 64y = 144
When the graph crosses the x- axis the y- coordinate of the point is zero.
Let y = 0 in the equation and solve for x
9x +0 = 144
9x = 144 ( divide both sides by 9 )
x = 16 ← x - intercept ⇒ (16, 0 )
When the graph crosses the y- axis the x- coordinate of the point is zero
let x = 0 in the equation and solve for y
0 + 64y = 144
64y = 144 ( divide both sides by 64 )
y =
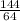 =
=
 ← y- intercept ⇒ (0,
← y- intercept ⇒ (0,
 )
)