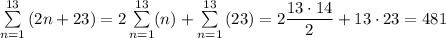Question

Find the sum of the odd integers between 24 and 50

Answer 1

481

Explanation:

There are several ways you can get there.

1. There are only 13 numbers, so you can write them down and add them up.

25 + 27 + 29 + ... + 47 + 49 = 481

__

2. You can use the formula for the sum of an arithmetic sequence. This one has a starting value of 25, an ending value of 49, and 13 terms.

Sum = ((start) + (end))/2 × (number of terms) = (25 +49)/2×13 = 481

__

3. You can use a formula for the terms of the series and evaluate the sum.

an = 25 +2(n -1) = 2n +23

`\sum\limits_(n=1)^(13){(2n+23)}=2\sum\limits_(n=1)^(13)(n)+\sum\limits_(n=1)^(13){(23)}=2(13\cdot 14)/(2)+13\cdot 23=481`