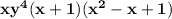Answer:
Factoring the expression
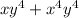 completely we get
completely we get
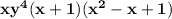
Explanation:
We need to factor the expression
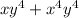 completely
completely
We need to find common terms in the expression.
Looking at the expression, we get
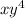 is common in both terms, so we can write:
is common in both terms, so we can write:
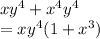
So, taking out the common expression we get:
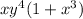
Now, we can factor the term (1+x^3) or we can write (x^3+1) by using formula:
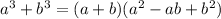
So, we get:
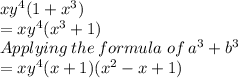
Therefor factoring the expression
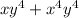 completely we get
completely we get