Question

find the equation of straight line which passes through the point of intersection of straight lines.x+2y+3=0 and 3x+4y=7 and parallel to the straight line y-x=8

Answer 1

Equation of the line in question:
`y = x - 21`.

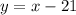Explanation:

Start by finding the intersection of the two straight lines. The equation for both lines shall hold at their intersection. (Using the idea of the Gaussian Elimination.)

`\left\{\begin{aligned}&x + 2y =-3\\&3x + 4y=7\end{aligned}\right.`.

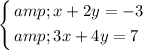Add -3 times the first equation to the second:

`\left\{\begin{aligned}&x + 2y =-3\\& -2y=16\end{aligned}\right.`.

Add the second equation
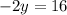`-2y=16` to the first:

`\left\{\begin{aligned}&x = 13\\&y=-8\end{aligned}\right.`.

Hence the intersection of the two lines will be
`(13, -8)`.

Now, find the slope of that straight line.
`y - x = 8` is equivalent to
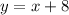`y = x +8`. The slope of that line is equal to 1. So will be the slope of the line in question.

Apply the point-slope form of a line on a Cartesian plane:

• Point:
  `(13, -8)`,
• Slope:
  `1`.

Equation of the line:

`(y - (-8)) = (x - 13)`.

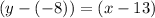Simplify to obtain:

`y = x -21`.