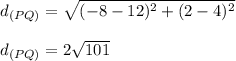Answer:
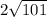
Explanation:
The distance between two points can be calculated with the following formula:

Given the points P(12, 4) and Q(-8, 2), we can identify that:
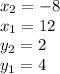
Then, substituing values into the formula, we get that the distance between these two points is: