Question

asked Mar 26, 2020 27.6k views

2 Answers

Vadim · Answer 1 · 2020-03-27T17:05:31+0000

Answer:

(4, 3).

Step-by-step explanation:

You just add the 2 components of the vectors.

(6,4) + (-2, -1) = (6 + -2, 4 + -1)

= (4, 3).

Jacquetta · Answer 2 · 2020-04-01T21:39:52+0000

Answer:

The resultant for given Vector A is (6, 4) and Vector B is (-2, -1) is 9.43.

The quantities which have both magnitude and direction is called vector.

The resultant is given by the formula:

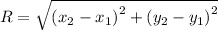
$R=\sqrt{\left(x_(2)-x_(1)\right)^(2)+\left(y_(2)-y_(1)\right)^(2)}$

Where,

R is resultant of the vectors A and B

x_1 ,
x_2 ,
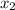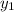y_1 , and
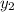y_2 are the vertices of vectors.

Given that:

x_1=6

x_2=-2

y_1=4

y_2=-1

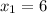
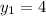
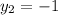
On substituting the given values in the above mentioned equation.

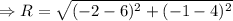
$\Rightarrow R=\sqrt{(-2-6)^(2)+(-1-4)^(2)}$

$\Rightarrow R=\sqrt{(-8)^(2)+(-5)^(2)}$

$\Rightarrow R=√(64+25)$

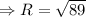
$\Rightarrow R=√(89)$

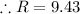
$\therefore R=9.43$

Therefore, resultant is 9.43 for the given vectors A and B.