Question

URGENT!!!!!Driving times for students' commute to school is normally distributed, with a mean time of 14 minutes and a standard deviation of 3 minutes. Using the empirical rule, approximately what percent of students' commute time is between 11 and 17 minutes? 32% 68% 95% 99.7%

Answer 1

Answer: 68%

Step-by-step explanation: ya boy just took le test :-)

Answer 2

B. 68%.

Explanation:

We have been given that driving times for students' commute to school is normally distributed, with a mean time of 14 minutes and a standard deviation of 3 minutes.

First of all, we will find z-score of 11 and 17 using z-score formula.

`z=(x-\mu)/(\sigma)`

`z=(11-14)/(3)`

`z=(-3)/(3)`

`z=-1`

`z=(17-14)/(3)`

`z=(3)/(3)`

`z=1`

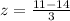
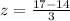
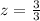
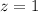
We know that z-score tells us a data point is how many standard deviations above or below mean.

Our z-score -1 and 1 represent that 11 and 17 lie within one standard deviation of the mean.

By empirical rule 68% data lies with in one standard deviation of the mean, therefore, option B is the correct choice.