Answer:
The parenthesis versus bracket thing is very important when entering your answer.
Interval part:
Domain: (-5,5]
Range: (2,3]
Inequality part:
Domain:
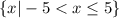
Range:
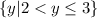
Explanation:
For domain, you read the graph from left to right.
The domain is all the x's where the relation exists.
We see that the line starts at x=-5 and ends at x=5.
We are NOT going to include x=-5 because there is a hole; this means immediately after x=-5 does the line exist.
We are going to include x=5 because the whole is filled which means our relation exists for x=5.
So an interval notation the domain is (-5,5].
The parenthesis means not to include the endpoint where the bracket mean to include.
The range is the y values for where the relation exists so you look from bottom to top or down to up.
So we see the first y is at y=2 (again there doesn't exist a point at y=2 because of the hole so we are going to have a parenthesis here which means not to include).
Reading up from there we see the last y that is reached is y=3 and we do include that point because the hole is filled.
So the range in interval notation is (2,3].
Assume
 is a smaller value than
is a smaller value than
 .
.
Now if you have the variable u is in the interval
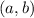 then the inequality is
then the inequality is
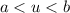 .
.
If the interval was
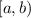 then it would be
then it would be
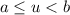
If the interval was
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png) then it would be
then it would be

If the interval was
![(a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qm4nt1slv5ncbz5nodff6jb9vin4wa4v4n.png) then it would be
then it would be
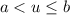
So if you haven't guessed it, if you see an equal part in your inequality than you will have a bracket for that number in the interval notation.
So let's look at our answers from above to find the inequality notation:
Domain: (-5,5]
Domain is the x's where the relation exists.
So this means we have
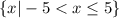 .
.
Range: (2,3]
Range is the y's where the relation exists:
So this means we have
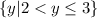 .
.