Question

In the diagrams below, ABC is similar to RST. Use a proportion with sides AB and RS to find the scale factor of ABC to RST. Show your work.

Answer 1

Answer: The required scale factor of ΔABC to ΔRST is
`(1)/(3).`

Step-by-step explanation: Given that triangles ABC and RST are similar, where

AB = 18, BC = 15, AC = 9 and RS = 6.

We are use a proportion with sides AB and RS to find the scale factor of triangle ABC to triangle RST.

We know that the scale factor of dilation is given by

`S=\frac{\textup{length of a side of dilated triangle}}{\textup{length of the corresponding side of the original triangle}}.`

Since AB and RS are corresponding sides of the two similar triangle ABC and RST, so the scale factor of ABC to RST is

`S=(RS)/(AB)\\\\\\\Rightarrow S=(6)/(18)\\\\\\\Rightarrow S=(1)/(3).`

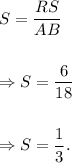
Thus, the required scale factor of ΔABC to ΔRST is
`(1)/(3).`

Answer 2

The scale factor of triangle ABC to triangle RST is 1/3

Explanation:

we know that

If two figures are similar, then the ratio of its corresponding sides is proportional and this ratio is called the scale factor

Let

z ----> the scale factor

To find the scale factor divide the length side of the image (reduced triangle) by the corresponding length side of the pre-image (original triangle)

`z=(RS)/(AB)`

substitute the values

`z=(6)/(18)`

simplify

`z=(1)/(3)`

The scale factor is less than 1

so

Is a reduction