Answer:
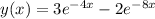
Explanation:
I will do the first one thoroughly so you won't have any problems following to complete the rest of them.
This is a linear homogeneous second order differential, so to solve it we will use:
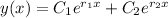 which is a theorem that says that if r1x and r2x are both solutions off a linear homogeneous equation, and C1 and C2 are any constants, then the function above is also a solution of the equation.
which is a theorem that says that if r1x and r2x are both solutions off a linear homogeneous equation, and C1 and C2 are any constants, then the function above is also a solution of the equation.
We need to solve for r1 and r2 using the differential equation:
y'' + 12y' + 32y = 0
Solve the differential equation for r1 and r2 by first replacing the y'' with r^2 and the y' with r:
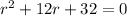
W will factor that now to solve for the 2 values of r:
(r + 4)(r + 8) = 0
By the Zero Product Property, either one of those binomials has to equal 0 for the product to equal 0, so
r + 4 = 0 and r = -4
r + 8 = 0 and r = -8
Those are the values for r1 and r2 and we can sub them back in to the y(x) equation:
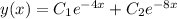
This we will call Equation 1.
Now we find the derivative of that equation, using the rules for finding derivatives of e's:

This we will call Equation 2.
Now we will use our first initial condition in Equation 1, where y(0) = 1:
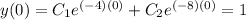
Simplifying gives you:
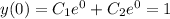 so
so
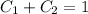
Now we will use the second initial condition in Equation 2, where y'(0) = 4:

Simplifying gives you:
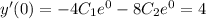 so
so
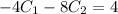
We will now go back to the first bold equation and solve it for C1:
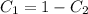 and sub that value in to the second bold equation to solve for C2:
and sub that value in to the second bold equation to solve for C2:
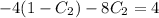 and
and
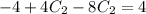 and
and
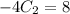 so
so
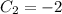
Now sub that back in to the first bold equation to solve for C1:
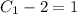 so
so
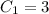
Finally we go back to the y(x) equation and fill everything in:
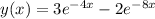
And that's your original equation! Follow this to the "t" and you'll have no problems with the other 2. They are identical in execution.