Question

The average cost per unit for the production of a certain brand of DVD is given by C=\frac{500+60c+0.01x^2}{x} , where x is the number of units produced.

The is a line _ over the C, don't know what that means.

A. What is the average cost per unit when 500 units are produced? 60 units? 100 units?

B. Is it reasonable to say that the average cost continues to fall as the number of units produced rises?

Answer 1

A: for 500: 66; for 60: 68.9; for 100: 66

B: no

Explanation:

We assume your average cost function is ...

`\overline{C}=(0.01x^2+60x+500)/(x)`

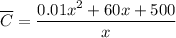
A. The overline over the C indicates it is an average value.

Evaluating the cost function at the different production levels, we find the average cost per unit to be ...

500 units

c = ((0.01·500)+60)500 +500)/500 = 65 +1 = 66

60 units

c = ((0.01·60 +60)·60 +500)/60 = 60.6 +500/60 ≈ 68.93

100 units

c = ((0.01·100 +60)·100 +500)/100 = 61 +5 = 66

__

B. Dividing out the fraction, we find that the cost per unit is ...

0.01x +60 +500/x

As x gets large, this approaches the linear function c = 0.01x +60. This increases as the number of units produced rises. (The minimum average cost is at a production level of about 224 units.)