Question

Suppose the solutions of a homogeneous system of six linear equations in nine unknowns are all linear combination of four linearly independent nonzero solutions. Will the system necessarily have a solution for every possible choice of constants on the right sides of the equations? Explain.

Answer 1

yes, system have a solution

Explanation:

Given data

linear equation = 6

unknown = 9

to find out

Will the system necessarily have a solution

solution

we multiply one non zero solution and we know that

A = 6 × 9 matrix

and n = 9

so dim (NulA) = 3

because we know (9-6) = 3

and rank of (A) = n - dim(NulA) = 9 - 3 = 6

so we say now here image of A i.e 6 dimensional subspace (A have 6 row)

so that Col (A) will be
`R^(6)`

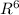
so its mean Ax = b has solution when we have b

so we now say that yes, system have a solution