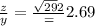Question

Find the approximate values of the trigonometric functions of θ given the following information. Enter the values correct to 2 decimal places. θ is in standard position the terminal side of θ is in quadrant III the terminal side is parallel to the line 2y - 5x + 16 = 0

sin θ =
cos θ =
tan θ =
cot θ =
sec θ =
csc θ =

Answer 1

Explanation:

slope of any line is same as the tan θ . so we first try to find the slope of the given line and then using that we can find remaining trigonometric functions .

To find the slope of a line we need to change the equation of line to slope intercept form .

2y - 5x +16 =0

move all terms to right

2y = 5x - 16

divide all by 2

y = 5/2 x - 8

compare this with y =mx+b

slope = m = 5/2

It means

tan θ = 5/2 = 2.5

tan θ = 2.50

now use the trigonometric ratios (see the image attached )

sin θ =
`(y)/(z) = (5)/(√(29) )  = 0.93`

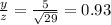
cos θ =
`(x)/(z) = (2)/(√(29) )  = 0.37`

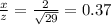
tan θ = 2.50

cot θ =
`(x)/(y) = (2)/(5 )  = 0.40`

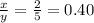
sec θ =
`(z)/(y) = \frac{√(29){5} }  = 1.08`

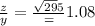
csc θ =
`(z)/(y) = \frac{√(29){2} }  = 2.69`