Question

Find the general explicit solution of the linear differential equation. Give the largest interval over which the general solution is defined. Determine if there are any transient terms in the general solution. dy/dx + y = e^3x

Answer 1

General explicit solution:
`y=(1)/(4)e^(3x)+Ce^(-x)`

Largest interval :
`(-\infty,\infty)`

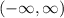
Transient term :
`e^(-x)`

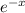
Explanation:

We are given that a linear differential equation

`(dy)/(dx) + y=e^(3x)`

We have to find the general explicit solution of given differential equation and largest interval on which the general solution is defined and transient term in the general solution.

Compare the given differential equation with general linear differentail equation of order 1

`(dy)/(dx) +P(x)y=Q(x)`

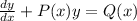
Then we get

P(x)=1 and Q(x)=
`e^(3x)`

Integration factor=
`e^(\int P(x) dx)=e^(\int1\cdot dx)=e^x`

`y* I.F=\int Q(x)\cdotI.F+ C`

`y* e^x=\int e^(3x)\cdot e^x dx+C`

`y\cdot e^x=\int e^(4x) dx+C`

`y\cdot e^x=(1)/(4)e^(4x) +C`

`y=(1)/(4)e^(4x)\cdot e^(-x)+Ce^(-x)`

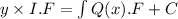
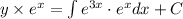
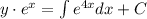
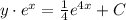
The general explicit solution in which dependent variable y depends on independent variable x.

Therefore, the general solution of linear differential equation

`y=(1)/(4)e^(3x)+Ce^(-x)`

Apply limit x tends to infinity

Then we get

`\lim_(x\rightarrow \infty)=(1)/(4) \lim_(x\rightarrow \infty)e^(3x)+C\lim_(x\rightarrow \infty)e^(-x)`

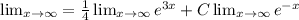
`e^(-\infty)=0` and
`e^\infty=\infty`

`y=\infty`

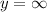
When x approach to -infinity

Then we get
`y=(1)/(4)\lim_(x\rightarrow- \infty)e^(3x)+C\lim_(x\rightarrow -\infty)e^(-x)`

`y=\infty`

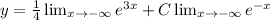
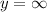
Hence, the largest interval on which solution of differential equation defined is
`(-\infty,\infty)`.

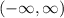To find the transient term

Transient term : when we apply x tends to infinity then any term of solution tends to zero then the term of solution is called transient term of solution.

When apply x tends to infinity then we get

`\lim_(x\rightarrow \infty)e^(-x)=0`

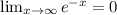
Hence ,
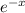`e^(-x)` is transient term of the solution.