Question

Let A be a set with 8 elements

a. find the number of subsets of A
b. find the number of subsets of A having one or more elements
c. find the number of subsets of A having exactly one element
d. find the number of subsets of A having two or more elements

Answer 1

a. The number of subsets of A is 256. b. The number of subsets of A with one or more elements is 255. c. The number of subsets of A with exactly one element is 8. d. The number of subsets of A with two or more elements is 248.

Step-by-step explanation:

a. The number of subsets of a set with n elements is 2^n. In this case, A has 8 elements, so the number of subsets of A is 2^8 = 256.

b. To find the number of subsets of A with one or more elements, we subtract the empty set from the total number of subsets. So the number of subsets of A with one or more elements is 256 - 1 = 255.

c. To find the number of subsets of A with exactly one element, we count the number of elements in A, which is 8.

d. To find the number of subsets of A with two or more elements, we subtract the number of subsets with exactly one element from the total number of subsets. So the number of subsets of A with two or more elements is 256 - 8 = 248.

Answer 2

a)The number of subsets of A is 256

b)The number of subsets of A having one or more elements is 255

c)The number of subsets of A having exactly one element is 8

d) The number of subsets of A having two or more elements is 247

Step-by-step explanation:

Let A be the set of 8 elements

Formula of number of subsets =
`2^n`

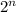
where n is the number of elements

Substitute n = 8

a) So, Number of subsets of A =
`2^8`

=
`256`

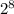
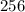
b)The number of subsets of A having one or more elements

Since the subsets contains ∅ also

So, we will exclude the null set

So, the number of subsets of A having one or more elements = Total no. of subsets - 1

=256-1

=255

c)The number of subsets of A having exactly one element

Since the no. of elements are 8 in Set A

So, The number of subsets of A having exactly one element = 8

d. The number of subsets of A having two or more elements

Since The number of subsets of A having exactly one element = 8

The subsets contains ∅ also

So, we will exclude null set and subsets of A having exactly one element

So, The number of subsets of A having two or more elements = 256-(8+1)

=247

Hence ,

a)The number of subsets of A is 256

b)The number of subsets of A having one or more elements is 255

c)The number of subsets of A having exactly one element is 8

d) The number of subsets of A having two or more elements is 247