Question

Solve the equation using the substitution u = y/x. When u = y/x is substituted into the equation, the equation becomes separable. Select the values for A, B, and C dy/dx=(xy+y^2)/(3x^2+y^2) becomes integral (u^2+A)/(u^3+Bu^2-4u)

Answer 1

`(u^2+3)/(-u^3+u^2-2u)u'=(1)/(x)`

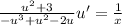
Explanation:

First step: I'm going to solve our substitution for y:

`u=(y)/(x)`

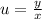
Multiply both sides by x:

`ux=y`

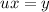
Second step: Differentiate the substitution:

`u'x+u=y'`

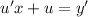
Third step: Plug in first and second step into the given equation dy/dx=f(x,y):

`u'x+u=(x(ux)+(ux)^2)/(3x^2+(ux)^2)`

`u'x+u=(ux^2+u^2x^2)/(3x^2+u^2x^2)`

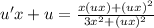
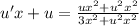
We are going to simplify what we can.

Every term in the fraction on the right hand side of equation contains a factor of
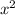`x^2` so I'm going to divide top and bottom by
`x^2`:

`u'x+u=(u+u^2)/(3+u^2)`

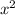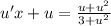
Now I have no idea what your left hand side is suppose to look like but I'm going to keep going here:

Subtract u on both sides:

`u'x=(u+u^2)/(3+u^2)-u`

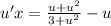
Find a common denominator: Multiply second term on right hand side by
`(3+u^2)/(3+u^2)`:

`u'x=(u+u^2)/(3+u^2)-(u(3+u^2))/(3+u^2)`

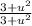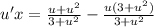
Combine fractions while also distributing u to terms in ( ):

`u'x=(u+u^2-3u-u^3)/(3+u^2)`

`u'x=(-u^3+u^2-2u)/(3+u^2)`

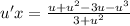
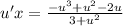
Third step: I'm going to separate the variables:

Multiply both sides by the reciprocal of the right hand side fraction.

`u' (3+u^2)/(-u^3+u^2-2u)x=1`

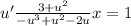
Divide both sides by x:

`(3+u^2)/(-u^3+u^2-2u)u'=(1)/(x)`

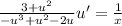
Reorder the top a little of left hand side using the commutative property for addition:

`(u^2+3)/(-u^3+u^2-2u)u'=(1)/(x)`

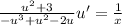
The expression on left hand side almost matches your expression but not quite so something seems a little off.