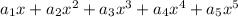Question

Find the kernel of the linear transformation. (If all real numbers are solutions, enter REALS.)

T: P5 → R, T(a0 + a1x + a2x^2 + a3x^3 + a4x^4 + a5x^5) = a0

Answer 1

Kernel is the set of all elements of the form

`a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5`

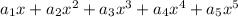
Explanation:

We are given that a linear transformation

T:
`P_5\rightarrow R`

`T(a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5)=a_0`

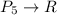
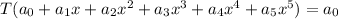
We have to find the kernel of the linear transformation if all real numbers are solutions

Kernel: It is defined as set of elements whose image is zero.

i.e T(x)=0 for any x belongs to domain.

To find the kernel of given linear transformation we substituting the given function is equal to zero

`T(a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5)=0`

`a_0=0`

Therefore, the basis of kernel of given linear transformation is

K=
`\left\{x,x^2,x^3,x^4,x^5\right\}`

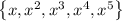
Kernel is the set of all elements of the form

`a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5`