Answer:
a) How many social security cards can be issued with no repeated digits?
We have 10 numbers from 0 to 9. When no digit is repeated, so we get 10! ways that is =

= 3628800
b) How many social security cards that can be issued with at least one digit repeated?
We will get this by subtracting 10! from all possible cases.
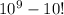
=
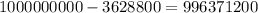
Exercise 4.
a) How many nonempty subsets are in a set of 5 elements?
Each element has 2 choices that are either selected in subset or not selected in subset.
Here, total choices will be
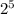
And it is 1 time that no element is selected.
So, the number of non empty subsets will be =

=>
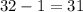
b) Erika has 5 friends. In how many ways can she invite one or more friends to a dinner party?
Same like above part, here Erika has two choices for each friend, either invite or not invite.
So, she has total
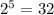 choices.
choices.
1 way to not invite anyone.
Hence, the number of ways can she invite one or more friends to a dinner party =
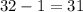 ways.
ways.