Question

Choose the Correct Feasible Region for the Following Constraints:

5X + 5Y < 80

2X + 6Y < 72

3X + 2Y < 42

X , Y > 0

Note: Some of these graphs look almost Identical, You will need to Create the Graph of the Feasible Region so you can Identify the Exact Corner Points.

Answer 1

area = 122 sq unit

Explanation:

Given constraints:

5X + 5Y < 80

2X + 6Y < 72

3X + 2Y < 42

X , Y > 0

To find the co-ordinates we can find

`(x)/(16) +(y)/(16) <1\\(x)/(36) +(y)/(12) <1\\(x)/(14) +(y)/(21) <1`

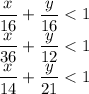
the co-ordinates are shown in the diagram

by solving equation

5X + 5Y < 80

3X + 2Y < 42

we will get the intersection point x = 10 and Y = 5

shaded region in the graph shows the required region

required area can be found out by

`area = \int_(0)^(10)(16-x)dx+\int_(10)^(14)(21-1.5x)dx`

`area=\left ( 16x-(x^2 )/(2)\right)^(10)_0 +\left ( 21x-(1.5x^2 )/(2)\right)^(14)_(10)`

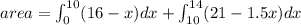
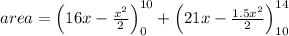
area = 122 sq unit