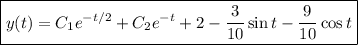Question

Find the general solution of the given differential equation 2y"' + 3y' +y= 2 + 3 sint

Answer 1

I suppose you meant to have the second derivative as the first term:

`2y''+3y'+y=2+3\sin t`

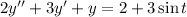
The corresponding homogeneous equation

`2y''+3y'+y=0`

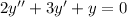
has characteristic equation

`2r^2+3r+1=(2r+1)(r+1)=0`

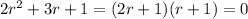
with roots at
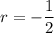`r=-\frac12` and
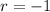`r=-1`, giving the characteristic solution

`y_c=C_1e^(-t/2)+C_2e^(-t)`

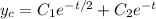
For the nonhomogeneous equation, assume a solution of the form

`y_p=a+b\sin t+c\cos t`

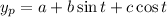
with derivatives

`{y_p}'=b\cos t-c\sin t`

`{y_p}''=-b\sin t-c\cos t`

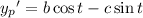
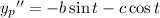
Substituting these into the ODE gives

`2(-b\sin t-c\cos t)+3(b\cos t-c\sin t)+(a+b\sin t+c\cos t)=2+3\sin t`

`-(b+3c)\sin t+(3b-c)\cos t+a=2+3\sin t`

`\implies a=2,b=-\frac3{10},c=-\frac9{10}`

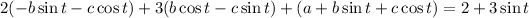
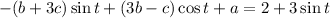
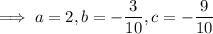
Then the ODE has solution

`\boxed{y(t)=C_1e^(-t/2)+C_2e^(-t)+2-\frac3{10}\sin t-\frac9{10}\cos t}`