Answer: The distance along the incline the mass slide from the point of release until it is brought momentarily to rest is 0.68 meter
Step-by-step explanation:
Let distance slide by block along the incline be L
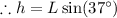
where h = initial height of block from the ground level
Since the inclined surface is frictionless so total mechanical energy is conserved for the spring-block system
Therefore applying conservation of mechanical energy we get
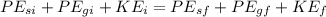
where
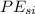 = Initial spring potential energy
= Initial spring potential energy
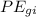 = Initial gravitational potential energy
= Initial gravitational potential energy
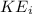 = Initial kinetic energy
= Initial kinetic energy
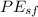 = Final spring potential energy
= Final spring potential energy
 =Final gravitational potential energy
=Final gravitational potential energy
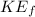 = Final kinetic energy
= Final kinetic energy
=>
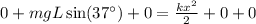
=>
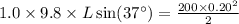

Thus the distance along the incline the mass slide from the point of release until it is brought momentarily to rest is 0.68 meter