Answer:
-1 is the inverse of 16 modulo 17.
Explanation:
To find : An inverse of 16 modulo 17 i.e.
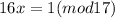 ?
?
Solution :
First we find the GCD of (17,16) using Euclid's algorithm,
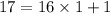
Remainder is 1.
Which means, GCD(17,16)=1
Using back substitution we get,
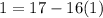
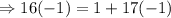
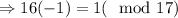
i.e. -1 is the inverse of 16 modulo 17.
On comparing with
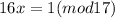
The value of x=-1.