Answer:
yes
Explanation:
We are given that a Cauchy Euler's equation
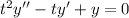 where t is not equal to zero
where t is not equal to zero
We are given that two solutions of given Cauchy Euler's equation are t,t ln t
We have to find the solutions are independent or dependent.
To find the solutions are independent or dependent we use wronskain

If wrosnkian is not equal to zero then solutions are dependent and if wronskian is zero then the set of solution is independent.
Let
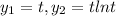
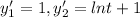
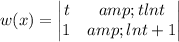
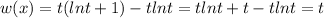 where t is not equal to zero.
where t is not equal to zero.
Hence,the wronskian is not equal to zero .Therefore, the set of solutions is independent.
Hence, the set {t , tln t} form a fundamental set of solutions for given equation.