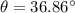Question

On a cold day, hailstones fall with a velocity of 2i − 6k m s−1 . If a cyclist travels through the hail at 10i m s−1 , what is the velocity of the hail relative to the cyclist? At what angle are the hailstones falling relative to the cyclist?

Answer 1

The velocity of the hail relative to the cyclist is
`V_(hc)=-8\hat{i}-6\hat{k}`

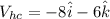
The angle at which hailstones falling relative to the cyclist is
`\theta = 36.86^\circ`

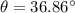
Explanation:

Given : On a cold day, hailstones fall with a velocity of
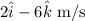`2\hat{i}-6\hat{k}\text{ m/s}` . If a cyclist travels through the hail at
`10\hat{i} \text{ m/s}`.

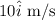To find : What is the velocity of the hail relative to the cyclist and At what angle are the hailstones falling relative to the cyclist?

Solution :

The velocity of the hailstone falls is
`V_h=2\hat{i}-6\hat{k}\text{ m/s}`

The velocity of the cyclist travels through the hail is
`V_c=10\hat{i} \text{ m/s}`

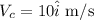
The velocity of the hail relative to the cyclist is given by,

`V_(hc)=V_h-V_c`

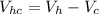
Substitute the value in the formula,

`V_(hc)=2\hat{i}-6\hat{k}-10\hat{i}`

`V_(hc)=-8\hat{i}-6\hat{k}`

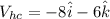
So, The velocity of the hail relative to the cyclist is
`V_(hc)=-8\hat{i}-6\hat{k}`

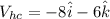
Now, The angle of hails falling relative to the cyclist is given by

`\theta = \tan^(-1)((-6)/(-8))`

`\theta = \tan^(-1)((3)/(4))`

`\theta = 36.86^\circ`

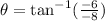
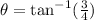
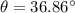
So, The angle at which hailstones falling relative to the cyclist is
`\theta = 36.86^\circ`