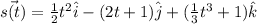Question

A particle moves with velocity vector

v(t) = ti - 2j + t^2 k

At time t = 0 the particle is at the point (0, −1, 1). What is the position of the particle at time t?

Answer 1

`\vec{s(t)}=(1)/(2)t^2\hat{i}-(2t+1)\hat{j}+((1)/(3)t^3+1)\hat{k}`

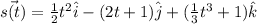
Explanation:

We are given that velocity vector of a particle

`\vec{v(t)}=t\hat{i}-2\hat{j}+t^2\hat{k}`

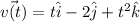
When t=0 then the particle is at the point (0,-1,1).

We have to find the position of particle at time t.

We know that

Velocity =
`(Displacement )/(time)=(ds)/(dt)`

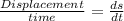
Therefore,
`\vec{v}=\frac{\vec{ds}}{dt}`

`\int{ds}=\int (t\hat{i}-2\hat{j}+t^2\hat{k})dt`

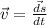
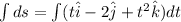
Integrate on both sides then we get

`\vec{s(t)}=(1)/(2)t^2\hat{i}-2t\hat{j}+(1)/(3)t^3\hat{k}+C`

`\int x^n dx=(x^(n+1))/(n+1)+C`

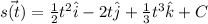
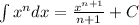
Substitute the value of point at time t=0 then we get

C=
`-\hat{j}+\hat{k}`

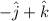
Substitute the value of C then we get

`\vec{s(t)}=(1)/(2)t^2\hat{i}-2t\hat{j}+(1)/(3)t^3\hat{k}-\hat{j}+\hat{k}`

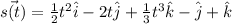
Therefore, the position of particle at time t

`\vec{s(t)}=(1)/(2)t^2\hat{i}-(2t+1)\hat{j}+((1)/(3)t^3+1)\hat{k}`