Answer:

Explanation:
We are given that velocity vector of a particle
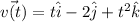
When t=0 then the particle is at the point (0,-1,1).
We have to find the position of particle at time t.
We know that
Velocity =
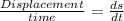
Therefore,
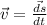
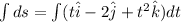
Integrate on both sides then we get
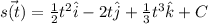
Substitute the value of point at time t=0 then we get
C=
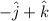
Substitute the value of C then we get
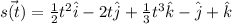
Therefore, the position of particle at time t
