Answer:
Explanation: (a) The balanced equation for the reaction of ammonia with HCl is written as:
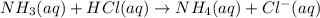
From the above equation, they react in 1:1 mol ratio. So, at equivalence point, their moles must be equal.
Moles = molarity * Liters
Let's convert mL of ammonia to L and multiply by given molarity to calculate its moles.
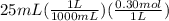
= 0.0075 moles of ammonia
At equivalence point, moles of HCl will also be 0.0075. Let's divide these moles by the given molarty of HCl to calculate its required volume to reach the equivalence point.
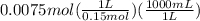
= 50.0 mL of HCl
So, 50.0 mL of HCl are required to reach the equivalence point.
(b) To reach the half equivalence point, exactly half volume of HCl that is 25.0 mL will be required.
So, at half equivalence point, out of 0.0075 moles of ammonia, only 0.00375 moles will be used to react with 0.00375 moles of HCl. 0.00375 moles of
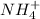 will form and the solution will act as a buffer solution as it has a weak base(ammonia) and its conjugate acid(ammonium ion).
will form and the solution will act as a buffer solution as it has a weak base(ammonia) and its conjugate acid(ammonium ion).
pH of buffer solution is calculated using Handerson equation:
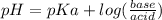
Since we have equal moles of ammonia(base) and ammonium ion(acid), the log part will be zero and then:
pH = pKa
pKa for ammonia is 9.25.
pH = 9.25
so the pH at the half equivalence point will be 9.25 and it indicates the solution will be basic.
(c) At equivalence point, we have 0.0075 moles of
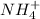 and the total volume of the solution is 75 mL (25 mL of ammonia and 50 mL of HCl) that 0.075 L.
and the total volume of the solution is 75 mL (25 mL of ammonia and 50 mL of HCl) that 0.075 L.
So, concentration of
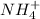 =
=

= 0.10 M
The equation for ammonium ion could be written as:
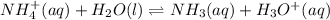
If the change in concentration is x then at equilibrium, the concentration of each of the product will be x and the concentration of
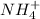 will be (0.10 - x).
will be (0.10 - x).
![Ka=([x][x])/([0.10-x])](https://img.qammunity.org/2020/formulas/chemistry/college/m617g3i0j1cy82v27pzqbs4x9dabjjtp93.png)
![Ka=([x]^2)/([0.10-x])</p><p>Ka for [tex]NH_4^+](https://img.qammunity.org/2020/formulas/chemistry/college/quvet00xcdzhqoufct3zjvy6nydzcbxqr9.png) is
is
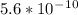 . It's a very low value so the x on the bottom could be neglected and the expression could be written as:
. It's a very low value so the x on the bottom could be neglected and the expression could be written as:
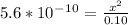
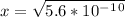
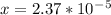
So, the concentration of
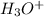 is
is
 M.
M.
pH = - log
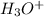
pH = - log

pH = 4.63
So, the pH at equivalence point will be 4.63 .
D) When 55 mL of HCl are added then moles of HCl will be:
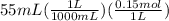
= 0.00825 moles of HCl
We have only 0.00750 moles of ammonia. So, excess moles of HCl = 0.00825 - 0.00750 = 0.00075 moles
Total volume = 55 mL + 25 mL = 80 mL = 0.08 L
Concentration of excess HCl in the solution =
 = 0.009375 M
= 0.009375 M
pH = - log 0.009375
pH = 2.03
So, the pH will be 2.03 when 55 mL of HCl has been added.
e) An indicator indicates the equivalence point of a titration by changing its color in the solution. From calculations of part c, the pH at equivalence point is 4.63. The best indicator is the one that changes color in the range of equivalence pH. pH range for methyl red, the pH range is 4.4 to 6.2 and the equivalence pH(4.63) falls in this range. So, the best indicator for this titration is methyl red.