Question

How many grams of CO-60 result in 1 Millicuire of activity? How many years until the activity decays to 1 microcuire tl/2 =5.3 Years

Answer 1

m =8.81*10^{-6}grams

time t = 52.8 year

Step-by-step explanation:

GIVEN DATA:

the half life of the CO-60 is, T_1/2 = 5.27 years = 1.663 e+8 s

activity dN/dt = 1 mCi = 3.7 X 10^7 decay/s

activity ,
`dN/dt = N* \lambda`

`(dN)/(dt) = N* (ln2)/(T_1/2)`

`N = ((dN/dt )(T1/2))/(ln2)`

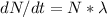
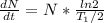
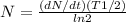
= ( 3.7 X 10^7 )(1.663*10^8 ) / ln2

= 8.877*10^{16}

Number of moles:

n = N/NA = 8.877*10^{16} / 6.022X10^23 = 1.474*10^{-7} mol

mass of the CO-60 is,

m = n*M = [1.474*10^{-7} mol]*[59.93 grams /mol] = 8.81*10^{-6}grams

-----------------------------------------------------------------------------------------

time t = -[T1/2 / ln2]*ln[N/N0]

= - [5.3 years / ln2]*ln[1x10-6/1x10-3]

= 52.8 year