Question

The muzzle velocity of a rifle bullet is 709 m s−1along the direction of motion. If the bullet weighs 35 g, and the uncertainty in its momentum is 0.20%, how accurately can the position of the bullet be measured along the direction of motion?

Answer 1

Uncertainty in position of the bullet is
`\Delta x=1.07* 10^(-33)\ m`

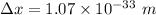
Step-by-step explanation:

It is given that,

Mass of the bullet, m = 35 g = 0.035 kg

Velocity of bullet, v = 709 m/s

The uncertainty in momentum is 0.20%. The momentum of the bullet is given by :

`p=mv`

`p=0.035* 709=24.81\ kg-m/s`

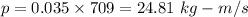
Uncertainty in momentum is,

`\Delta p=0.2\%\ of\ 24.81`

`\Delta p=0.049`

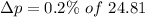
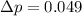
We need to find the uncertainty in position. It can be calculated using Heisenberg uncertainty principal as :

`\Delta p.\Delta x\geq (h)/(4\pi)`

`\Delta x=(h)/(4\pi \Delta p)`

`\Delta x=(6.62* 10^(-34))/(4\pi * 0.049)`

`\Delta x=1.07* 10^(-33)\ m`

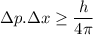
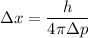
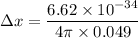
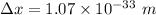
Hence, this is the required solution.